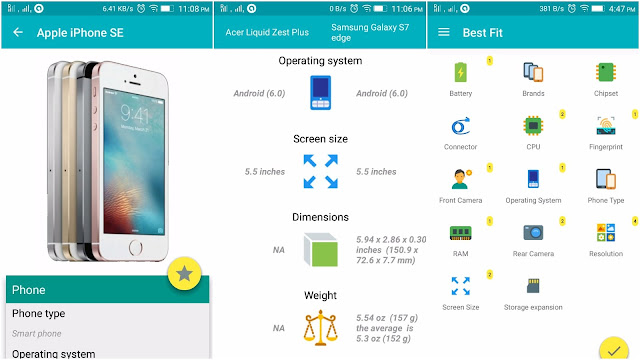
What is a Tensor Rank and Tensor Shape - TensorFlow
In this article, we will learn about Tensor Ranks and Tensor Shapes.
We know a tensor is an n-dimensional array. So, Rank is defined as the number of dimensions of that tensor. And, Tensor Shape represents the size of the each dimension.
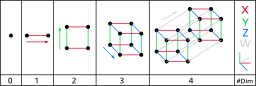
A tensor with rank 0 is a zero-dimensional array. The element of a zero-dimensional array is a point. This is represented as a Scalar in Math and has magnitude.
Eg:
s = 48.3
Shape -
A tensor with rank 1 is a one-dimensional array. The elements of the one-dimensional array are points on a line. This line has magnitude, direction. and is represented as Vector in Math. Vector has n entries.
[]A tensor with rank 1 is a one-dimensional array. The elements of the one-dimensional array are points on a line. This line has magnitude, direction. and is represented as Vector in Math. Vector has n entries.
Eg: v = [1, 9, -6, 7, 0]
Shape -
[5]A tensor with rank 2 is a two-dimensional array. The elements of the two-dimensional array are lines on a surface. This surface is represented as a Matrix in Math and has two coordinates. The Matrix contains n x n entries.
Eg:
m = [[2.4, 5.1], [3.3, 7.9], [8.5, 6.1]]Shape -
[3, 2]Eg:
t = [[[2, 5, 6], [5, 3, 3], [6, 7, 8]], [[0, 0, 1], [9, 7, 9], [2, 3, 6]], [[4, 8, 2], [1, 0, 8], [4, 4, 0]]]Shape -
[3, 3, 3]You can continue increasing the entries to create a 4-Tensor, 5-Tensor, .... n-Tensor. n-Tensor has n x n x n x n .... n entries, while it's shape is
[n, n, n, n, n, ... n]Below is the code snippet that creates tensors with different ranks and shapes. Play with it.